Significant figures (sig figs) are essential for expressing measurement precision in science, particularly in chemistry. Knowing how to count significant figures in numbers like 100, 100., and 100.00 ensures accurate data reporting and calculations. This comprehensive guide explores the number of significant figures in these numbers, explains how to determine significant figures, and addresses common questions like how many sig figs in 100 or how many significant figures in 100.0. With practical examples, rules for rounding significant figures, and tips for handling trailing zeros significant figures, you’ll master significant figures examples and their applications in significant figures for chemistry.
What Are Significant Figures?
Significant figures represent the reliable digits in a measurement, reflecting its precision. For example, a ruler marked in centimeters is certain to the nearest centimeter, but its precision may extend to one decimal place with some uncertainty. In significant figures in chem, the correct number of significant figures ensures calculations align with measurement accuracy. Exact numbers (e.g., “3 people” or “1/2” in a formula) are considered to have infinite significant figures for calculations, but measured values like 100, 100., or 100.00 follow specific rules for significant figures.
This article focuses on how to calculate significant figures for 100, 100., and 100.00, using significant figures digits to clarify their precision.
Counting Significant Figures in 100
The number 100 is a common example in significant figures practice, often causing confusion due to its trailing zeros. To answer how many sig figs in 100 or how many significant figures in 100, apply the rules for determining significant figures:
Result: 100 has one significant figure (1).
Example Context
If a scale measures to the nearest 100 grams, 100 reflects one sig fig, indicating limited precision. If written as 100₂ (underlining the second digit, as in some notations), it could imply two sig figs, but standard notation assumes one sig fig unless specified otherwise.
Counting Significant Figures in 100.
The number 100. (with a trailing decimal point) changes the significant figure count due to the decimal’s presence. For how many sig figs in 100.:
Result: 100. has three significant figures (1, 0, 0).
Example Context
In significant figures in chemistry, a measurement of 100. mL on a graduated cylinder suggests precision to the nearest whole milliliter, with the zeros counted as significant. This aligns with significant figures decimals rules.
Counting Significant Figures in 100.00
The number 100.00 includes a decimal point and trailing zeros, making it a precise measurement. For how many significant figures does 100.0 have (extending to 100.00):
Result: 100.00 has five significant figures (1, 0, 0, 0, 0).
Example Context
A digital balance reading 100.00 grams in a lab implies five sig figs, reflecting precision to the hundredth of a gram. This demonstrates trailing zeros significant figures in action.
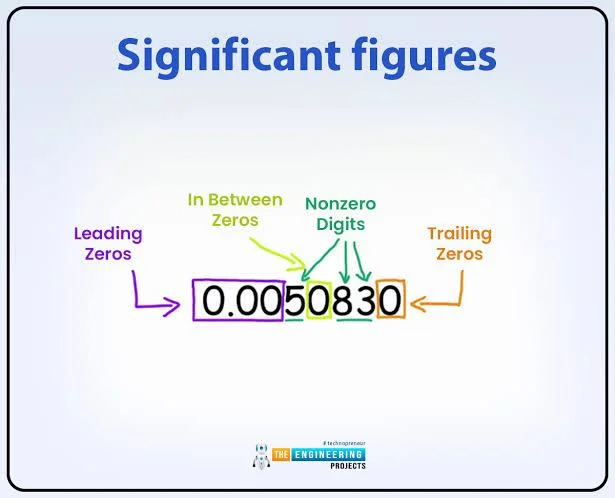
Rules for Counting Significant Figures
To generalize how to count significant figures, here are the core significant figures rules from Group 4, applied to numbers like 100, 100., and 100.00:
- Non-zero digits are always significant: Digits 1–9 count (e.g., 123 has three sig figs).
- Zeros between non-zero digits are significant: Zeros between digits count (e.g., 1002 has four sig figs).
- Leading zeros are not significant: Zeros before the first non-zero digit are ignored (e.g., 0.0062 has two sig figs).
- Trailing zeros are significant with a decimal point: Zeros after a decimal are significant (e.g., 8.50 sig figs: three).
- Trailing zeros without a decimal are ambiguous: Typically not significant unless noted (e.g., how many sig figs in 1000: one).
These rules clarify significant figures digits and are essential for significant figures in chem.
Significant Figures in 100, 100., and 100.00
| Number | Significant Figures | Count | Notes |
| 100 | 1 | 1 | Trailing zeros not significant without decimal |
| 100. | 1, 0, 0 | 3 | Zeros up to decimal are significant |
| 100.00 | 1, 0, 0, 0, 0 | 5 | Trailing zeros after decimal are significant |
This table summarizes sig fig examples for quick reference.
Rounding to Significant Figures
Rounding numbers like 100 or related values to a specific number of significant figures (e.g., round to 3 sig figs) is common in scientific calculations. The process for rounding significant figures is:
- Identify the required number of significant figures.
- Take the first digits up to that number.
- Round based on the next digit: 5 or higher rounds up, lower stays the same.
- Adjust zeros based on the number’s format.
Example 1: Rounding Examples
- Round to 2 significant figures for 233.356: First two digits are 2, 3; next is 3, so 230 (two sig figs).
- Round 0.00097 to 1 significant figure: First digit is 9; next is 7, so 0.001 (one significant figure).
- Round to 3 significant figures for 4.5678: First three digits are 4, 5, 6; next is 7, so 4.57 (three sig figs).
These examples illustrate how to round to significant figures and significant figures round.
Handling Zeros: Leading and Trailing
Zeros are a common source of confusion in significant figures decimals. Let’s clarify leading zeros sig figs and trailing zeros significant figures:
- Leading zeros: Not significant, as they set the decimal place (e.g., how many sig figs is 0.002: one).
- Trailing zeros: Significant only with a decimal (e.g., 10.0 sig figs: three; how many sig figs in 10: one).
Example 2: Zeros in Specific Numbers
- How many sig figs does 200 have: Two sig figs (2, 0), as trailing zeros without a decimal are not significant.
- How many sig figs in 2.0: Two sig figs (2, 0).
- How many sig figs in 2.00: Three sig figs (2, 0, 0).
- How many sig figs in 20: Two sig figs (2, 0).
- How many sig figs in 5.00: Three sig figs (5, 0, 0).
- Is the zero before a decimal a sig fig: No, as in 0.0419 sig figs (three: 4, 1, 9).
These cases highlight sig figs with decimals and decimals and significant figures.

More Specific Number Examples
Let’s explore additional numbers from Group 4 to reinforce how to know how many sig figs to use:
- How many sig figs in 1000: One sig fig (1), as trailing zeros are not significant.
- How many sig figs are in 1000: Same, one sig fig.
- 110. sig figs: Two sig figs (1, 1), as the trailing zero is not significant.
- 21.50 sig figs: Four sig figs (2, 1, 5, 0).
- 490.0 how many sig figs: Four sig figs (4, 9, 0, 0).
- 8.50 sig figs: Three sig figs (8, 5, 0).
- 4.00 sig figs: Three sig figs (4, 0, 0).
- How many significant figures in 1.00: Three sig figs (1, 0, 0).
- How many sig figs does 1.100 have: Four sig figs (1, 1, 0, 0).
- 1.0000 significant figures: Five sig figs (1, 0, 0, 0, 0).
- 3.00 significant figures: Three sig figs (3, 0, 0).
These examples of significant figures show the importance of context in significant figures 2, significant figures 3, and four significant figures.
Chemistry Applications
In significant figures in chemistry, precise counting of sig figs is vital for lab measurements. For example, a volume of 100.00 mL in a titration reflects five sig figs, ensuring accurate molarity calculations. Similarly, 100. mL indicates three sig figs, suitable for less precise instruments.
Example 3: Chemistry Measurement
A balance reads 0.052 g (two sig figs). Reporting this as 0.05 (one sig fig) via rounding numbers significant figures reduces precision unnecessarily, affecting subsequent calculations.
Common Mistakes in Counting Significant Figures
Practice Problems
Test your skills with these significant figures practice problems:
- How many sig figs in 0.01: Two sig figs.
- Round to 3 sig figs for 45.678: 45.7.
- How many sig figs in 10.0: Three sig figs.
- How many significant figures in 1000: One sig fig.
- 4.51-2.1395 in correct sig figs: Result is 2.37 (three sig figs).
These align with examples for significant figures and proper number of significant figures.
Tools for Counting Significant Figures
Use a significant figures calculator or sig fig counter to verify counts. A 3 sig fig calculator can confirm round to 3 significant figures results, as noted in Group 3.
Conclusion
Understanding significant figures in 100, 100., and 100.00 is key to mastering counting and rounding significant figures. By applying how to count sig figs and rounding numbers to significant figures, you ensure accuracy in significant figures for chemistry. Practice with sig figs examples, use tools like a significant figures counter, and explore related articles on significant figures rules or scientific notation with significant figures for deeper insights.

